Motor
Recomendamos o software Variation Analysis - VA, da Siemens, para calcular os valores das tolerâncias e dos índices da capacidade Cp/Cpk utilizados para avaliar orisco de não conformidade das características críticas, veja o exemplo abaixo.
Bons produtos começam por bons projetos
Desenvolver produtos melhores e mais baratos do que os concorrentes é vital. O objetivo é “fazer certo na primeira vez”. A rapidez também conta porque é preciso chegar ao mercado em primeiro lugar.
Bons projetos reduzem o custo e garantem qualidade. Não se espera o produto entrar em produção para pensar em qualidade. Deve-se garantir ZERO defeito no desenvolvimento dos novos produtos.
Bons produtos não são obra do acaso. Para desenvolvê-los é preciso usar as tecnologias QFD, Cotação Funcional, GD&T, Simulação Monte Carlo e Elementos Finitos.
Bons produtos são consequências de bons projetos, que por sua vez, sob o ponto de vista dimensional, são consequências de boas cotagens.
A cotagem é uma etapa muito importante do projeto mecânico por ser o elo entre a concepção do produto e a sua materialização. Não basta fazer o modelo 3D, é preciso cotá-lo adequadamente.
Para impedir a propagação dos erros dimensionais e geométricos a cotagem deve ser funcional, caso contrário será preciso apertar as tolerâncias. As peças não devem ser cotadas isoladamente, sem levar em conta o processo de montagem. A solução é criar a menor cadeia dimensional possível, com um vetor cota por peça.
Tendo em vista as fases seguintes ao projeto, que são a manufatura e a metrologia, usa-se o conceito Model Based Definition - MBD, que consiste em anexar todas as informações requeridas pela manufatura e controle ao modelo 3D, em particular o GD&T.
O MBD é o único formato admissível para a definição digital do produto.
Atende as normas ASME Y14.5, Y14.41 e Boeing D6-51991. Como o modelo 3D é a fonte única de informações não é mais necessário fazer desenhos 2D.
Veja abaixo um caso com emprego das diversas ferramentas de projeto
A pesquisa realizada para identificar os desejos dos consumidores deste motor revelou que ele deve ser silencioso.
Usa-se a ferramenta Quality Function Deployment – QFD para desdobrar os desejos dos consumidores e estabelecer as ações necessárias para realizá-los.
Veja o diagrama QFD abaixo.
• O primeiro passo é inserir "silencioso" no diagrama.
• A seguir identificam-se os geradores de ruído existentes no motor, sendo o "ruído de correia“ um dos principais. Ao seu lado coloca-se uma seta apontada para baixo, sinalizando que ele deve ser reduzido.
• Depois se faz a correlação entre os desejos e as características físicas.
• Os círculos vermelhos indicam que há uma forte correlação do ruído da correia com o paralelismo das polias e com a deformação do corpo da bomba d'água.
• Acrescentam-se os valores alvos, a tolerância e o Cp, índice de capacidade do processo, que é usado para medir o risco de não conformidade assumido pelos projetos relativamente aos desejos dos consumidores.
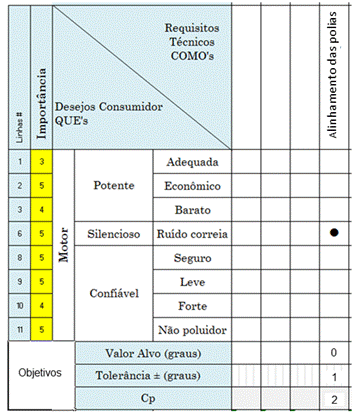
O Cp define o risco que o projeto assume quanto ao atendimento dos desejos do consumidor, que vem a ser a qualidade do produto.
Há uma correlação entre Cp e qualidade. Por exemplo, se a diretriz do projeto definir Cp=2, o risco assumido pelo projeto é de 3,4 não conformidades por milhão.
O passo seguinte é a cotagem funcional dos componentes, que é feita utilizando-se o GD&T - Geometric Dimensioning & Tolerancing.
Observa-se que o ruído de correia é provocado pelo desalinhamento das polias, que por sua vez é resultante das variações dimensionais e geométricas das diversas peças, dentre elas a bomba d’água.
Vê-se abaixo o MBD da bomba d’água.
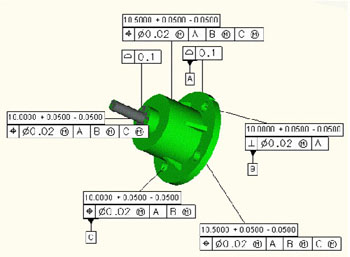
Os demais componentes também são cotados funcionalmente para estabelecer a cadeia de tolerâncias da polia.
A seguir executa-se a simulação Monte Carlo
A missão da simulação Monte Carlo é ajustar as tolerâncias para obter os valores de Cp / Cpk estabelecidos pela diretriz do projeto. Usa-se um software específico, que combina os possíveis valores das tolerâncias dimensionais e geométricas dos componentes e analisa a variação provocada no ângulo da polia.
Primeira Simulação
O resultado da simulação é apresentado em uma tela com os valores Cp/Cpk, veja na figura abaixo.
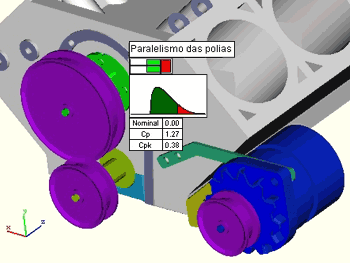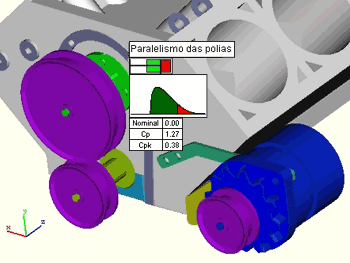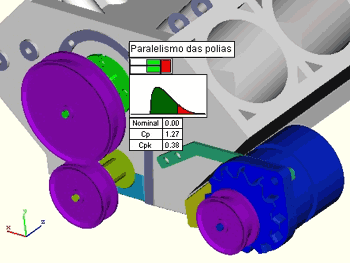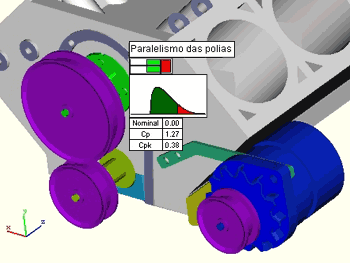
Como o valor do Cp ficou aquém do especificado será preciso apertar as tolerâncias.
Veja abaixo o relatório com as demais informações da primeira simulação Monte Carlo.
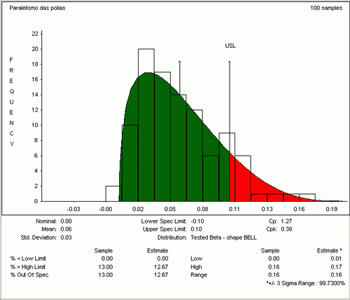
Alguns valores do relatório acima: Cp = 1.27 Cpk = 0.43 % Out Of Spec = 9%. Se os motores forem fabricados com estas tolerâncias haverá 9% de não conformidades, o que recomenda apertar as tolerâncias.
O software oferece outro relatório com as tolerâncias que afetam o ângulo da polia listadas pela ordem de importância.
Relação de tolerâncias da primeira simulação.
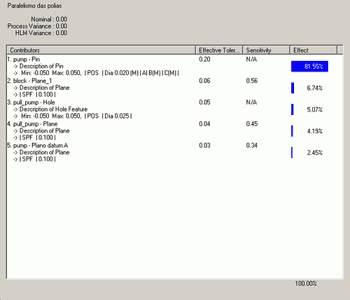
Observa-se que a tolerância que está no topo da relação é responsável por 81% da variação do ângulo da polia. Esta informação é muito valiosa porque vai direto a raiz do problema dimensional e aponta a causa principal.
A tolerância indicada em primeiro lugar deverá ser apertada e uma nova simulação Monte Carlo realizada.
Segunda simulação Monte Carlo
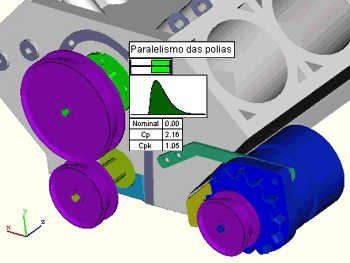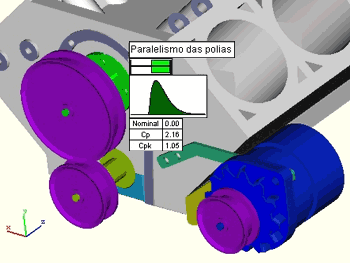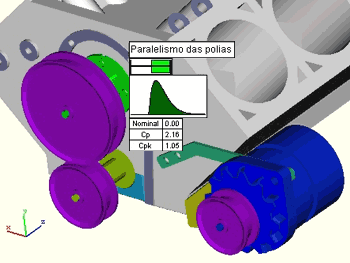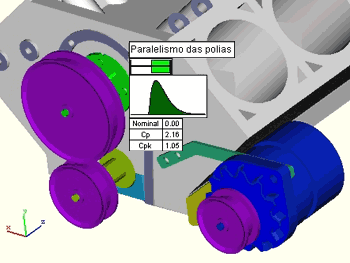
Ao terminar a simulação o programa apresenta uma tela com o resultado encontrado. Neste caso o valor Cp = 2.16 atende a especificação do diagrama QFD.
Se as peças forem fabricadas com estas tolerâncias pode-se garantir que o número de não conformidades será inferior a 3.4 / milhão.
Veja abaixo o relatório com as demais informações da segunda simulação Monte Carlo.
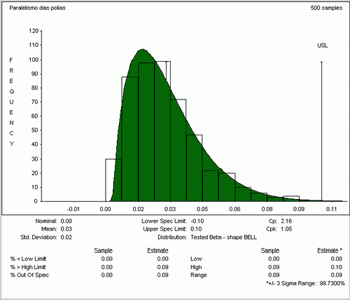
Alguns valores do relatório: Cp = 2.16 / Cpk = 1.07 / % Out Of Spec = 0.
Com estas tolerâncias o ângulo da polia ficará dentro do valor especificado e não haverá “ruído de correia” de acordo com os desejos dos consumidores.
A simulação Monte Carlo usa o método das aproximações sucessivas. A cada rodada ajusta-se a tolerância indicada e repete-se a simulação até o Cp alcançar o valor estabelecido no diagrama QFD. O conjunto final de tolerâncias representa a solução de compromisso ideal entre custo e qualidade.
Sob o ponto de vista dimensional o projeto seis sigma está terminado, mas é preciso verificar se a deformação dos componentes compromete o paralelismo das polias.
MEF - Método dos Elementos Finitos
A missão do MEF é identificar e resolver os problemas de resistência dos materiais. Neste caso é preciso saber se o aperto da correia deforma o corpo da bomba d'água e compromete o paralelismo das polias.
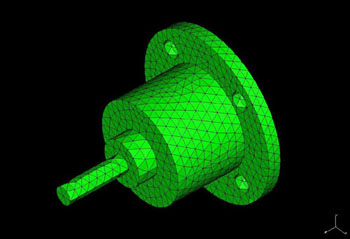
Inicialmente cria-se uma malha como mostra a figura acima.
A seguir aplica-se a carga provocada pelo aperto da correia.
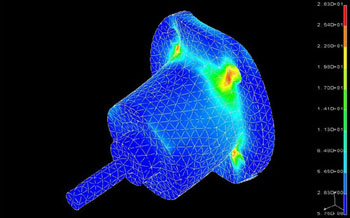
Observa-se que sob o efeito da carga a peça se deformou além do limite admissível e pode compromete o alinhamento das polias.
Uma das possíveis soluções é reforçar a carcaça para impedir a deformação excessiva. Foram acrescentadas quatro nervuras, como mostra a figura abaixo.
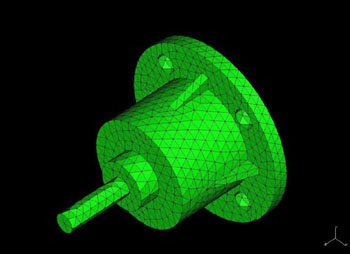
A seguir aplica-se nova carga à carcaça.
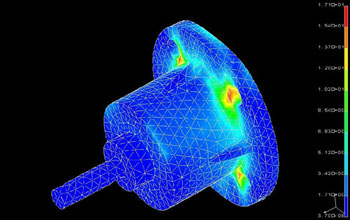
Observa-se que os reforços deram bom resultado. A deformação da carcaça ficou dentro dos limites admissíveis e não vai contribuir significativamente no paralelismo das polias. A simulação da variação estrutural dos componentes permite fazer previsões a respeito do seu comportamento e efetuar as devidas correções, antes da execução do protótipo físico, proporcionando economia de material e ferramental. Ensinamos as tecnologias acima e prestamos serviços. Entre em contato, teremos o maior prazer em ajudá-los a desenvolver projetos competitivos.
